Napětí a proud je v analogovém laboratorním zdroji nastavován pomocí potenciometrů. V procesorem řízeném zdroji, práci potenciometrů vykonávají DA převodníky. Místo abychom otáčeli potenciometrem, budeme otáčet rotačním kodérem. Procesor zpracuje údaj z rotačního kodéru a na DA převodník pošle číslo, které převodník převede na napětí. Napětí z převodníku je pak v analogové části zdroje použito k nastavení výstupního napětí na svorkách, nebo maximálního proudu na svorkách.
 

A k čemu to celé je?

• Rozlišení převodníků a rotačního kodéru může být velmi jemné. V našem zapojení můžeme rotačním kodérem nastavovat napětí po milivoltech a proud po miliampérách. Potenciometry by pro stejnou úlohu musely být víceotáčkové, nebo bychom museli použít dva, pro hrubé a jemné nastavení.
• Často používané hodnoty, např. 5,000V, 12,000V mohou být připraveny v paměti procesoru, není potřeba manipulovat s potenciometry.
• V případě použití potenciometrů, měřidla zdroje zobrazují jenom to, co je na svorkách. V případě použití procesoru můžeme na displeji zobrazit nejenom naměřenou, ale i nastavenou hodnotu. To má smysl hlavně u proudu, abych znal nastavení proudové pojistky analogového zdroje, musím jej zkratovat.
• Procesor může řídit hodnotu napětí a proudu sám, podle nějakého algoritmu. Například pro nabíjení baterií.
• Pomocí programu v procesoru můžeme korigovat linearitu analogového obvodu, případně teplotní závislost nastavených hodnot.

Celkem budeme potřebovat čtyři funkce:

• Na rotačním kodéru nastavíme a na displeji zobrazíme požadované napětí, proměnnou Voltage1_DaMilivolt. Rozlišení bude 1mV na dílek rotačního kodéru. Z tohoto nastaveného napětí vypočítáme údaj pro DA převodník, proměnnou Voltage1_DaOutput.
• AD převodník změří napětí na svorkách zdroje a procesor hodnotu uloží do proměnné Voltage1_AdInput. Z tohoto údaje vypočítáme napětí, proměnná Voltage1_AdMilivolt. To bude zobrazeno na displeji.
• Na rotačním kodéru nastavíme a na displeji zobrazíme požadovaný maximální proud, proměnnou Current1_DaMiliamper. Rozlišení bude 1mA na dílek rotačního kodéru. Z tohoto nastaveného proudu vypočítáme údaj pro druhý DA převodník, proměnnou Current1_DaOutput.
• Druhý AD převodník změří pomocí bočníku proud na výstupních svorkách zdroje a procesor získanou hodnotu uloží do proměnné Current1_AdInput. Z tohoto údaje vypočítáme proud, proměnná Current1_AdMiliamper. To bude zobrazeno na displeji.

Funkce pro DA převodník napětí

Námi použitý DA převodník DAC8563 má rozlišení 16-bitů a je napájen referenčním zdrojem 2,5V. Převodník rozdělí napětí 2,5V na 65536 dílků. Jeden dílek převodníku má tedy velikost 0,038mV.

Zdroj má být použit do 50,000V. Teď jsou dvě možnosti:

• Analogovou část zdroje uspořádáme tak, aby jeden dílek DA převodníku zesílila z 0,038147mV přesně na 1mV. DA převodník pak bude využíván od 0 do 50000 dílků a nebude potřeba nic počítat. Toto řešení bude náročné na analogovou část a bez počítání nepůjdou dělat korekce teplotní závislosti. Bude potřeba řešit nejenom přesné zesílení, ale i offset obvodu.
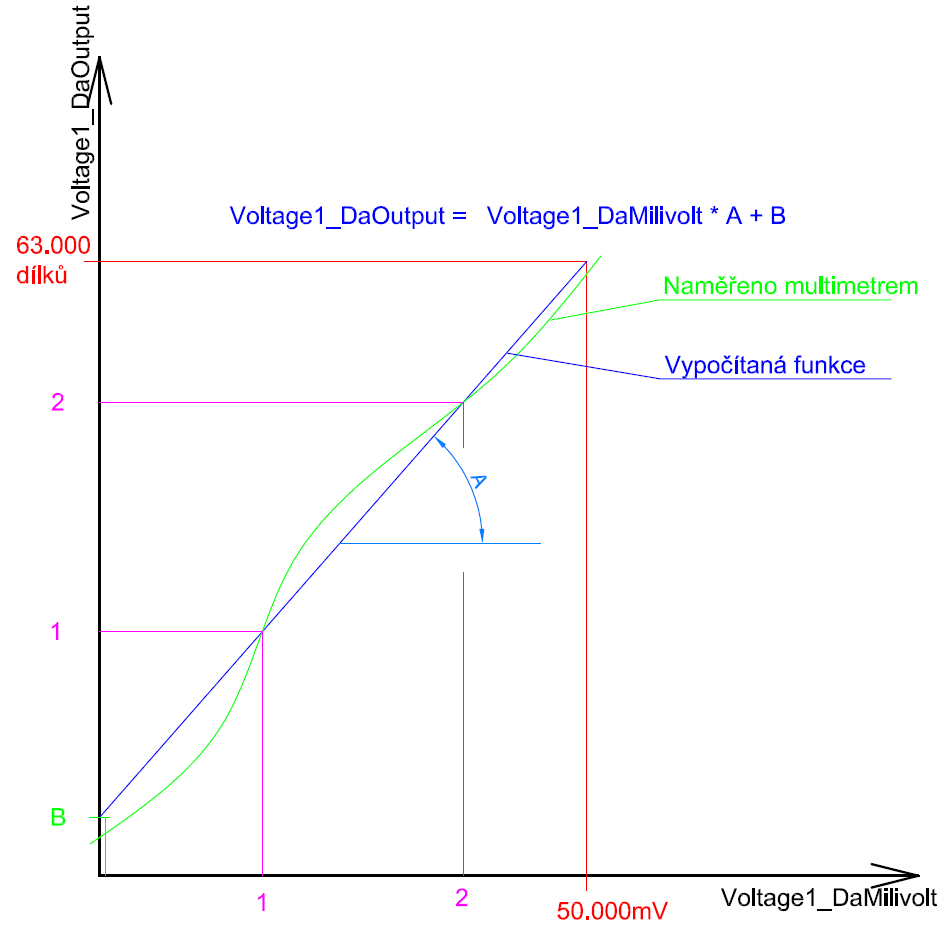
• Analogovou část zdroje uspořádáme tak, abychom převodník využili skoro v celém rozsahu, takže 50V bude někde kolem 63000 dílků. No a údaj z rotačního kodéru v milivoltech vynásobíme nějakou konstantou, abychom získali počet dílků pro DA převodník.

My se rozhodli použít druhou možnost. Procesor má dost velký výkon, aby mohl počítat mnohokrát za sekundu. Při řešení analogové části se budeme zabývat její stabilitou, zesílení nastavíme pomocí odporů ve zpětných vazbách operačních zesilovačů odhadem. Offset nebudeme v analogové části řešit vůbec. Prozatím budeme předpokládat, že závislot údaje na DA převodníku a napětí na výstupních svorkách je lineární. Takže funkce, kterou hledáme je rovnicí přímky a má následující podobu:

Voltage1_DaOutput = Voltage1_DaMilivolt * A + B

Koeficient A nastaví počet dílků DA převodníku na 1mV – určuje úhel přímky, která v grafu vyjadřuje závislost dílků převodníku na napětí. Koeficient B posune přímku grafu ve svislém směru, koriguje offset analogové části zdroje.
 

Abychom mohli vypočítat koeficienty lineární funkce, nastavíme na DA převodníku postupně dvě hodnoty a na výstupních svorkách zdroje změříme příslušné napětí:

10 000 dílků převodníku ⇒ 7 669 milivoltů na svorkách

20 000 dílků převodníku ⇒ 15 310 milivoltů na svorkách

Z těchto dvou bodů náhodně zvolených v rozsahu DA převodníku sestavíme rovnici přímky:

M = [ Mx; My ] = [ 7 669; 10 000 ]

N = [ Nx; Ny ] = [ 15 310; 20 000 ]

Vypočteme vektor přímky u = ( Nx – Mx; Ny – My) = ( 7 641; 10 000 )

Rovnice přímky jsou:

X = Mx + u1 * t

Y = My + u2 * t

Dosadíme: X = 7 669 + 7641 * t

Y = 10 000 + 10 000 * t, z toho t = ( Y – 10 000 ) / 10 000

Rovnici t = ( Y – 10 000 ) / 10 000 dosadíme do

X = 7 669 +( 7 641 * Y – 76 410 000 ) / 10 000

Postupně zjednodušíme:

10 000 * X = 280 000 + 7 641 * Y

X = 28 + 0,7641 * Y

0,7641 * Y = X – 28

Y = 1,3087 * X – 37

X je nezávislá proměnná, v našem případě milivolty nastavené na rotačním kodéru. Y je závislá proměnná, v našem případě dílky DA převodníku. Rovnice, která vypočítá ze zadaných milivoltů počet dílků DA převodníku je tady:

Voltage1_DaOutput = Voltage1_DaMilivolt * 1,3087 – 37
 

Programování rovnice na osmibitovém mikroprocesoru

Vstupní i výstupní proměnná rovnice je v množině celých čísel v rozmezí 0 – 65535, takže tyto proměnné budou deklarovány jako unsigned int. Koeficient 37 je celé číslo, sčítání bude fungovat v množině celých čísel. Nyní je několik možností a myšlenek, které budeme potřebovat k použití desetinného čísla 1,3087:

První úvaha bude o tom, jaký vliv má počet desetinných míst na výsledek výpočtu. Vstupní i výstupní hodnota výpočtu má v desítkové soustavě 5 míst. Abychom nesnížili přesnost výpočtu, je nutné, aby i koeficient kterým násobíme, měl 5 míst. Když bude mít menší počet míst, rozlišení výsledku bude menší, než rozlišení vstupní hodnoty. Výpočet nebude přesný, nebude využito původní rozlišení převodníku 16 bitů. Když bude mít koeficient větší množství míst než 5, bude to zbytečné. Výsledek bude mít sice víc desetinných míst, ale ty nebudou mít význam.

Tím, že hodnotu z 16-ti bitového převodníku vynásobím číslem 1,3087468912 sice získám číslo přes celý displej kalkulačky, ale vypočítaná hodnota přesnější než 16 bitů nebude. Počet desetinných míst na kalkulačce nerozhoduje o přesnosti čísla.

Při programování je nejjednodušší vzít knihovnu float.h a výpočet provést v množině čísel s pohyblivou desetinnou čárkou. Jenomže čísla z naší rovnice pohyblivou desetinnou čárku nemají. Vstup a výstup je celé číslo a koeficient má pevný počet desetinných míst. Tak to zkusíme jinak.

Koeficient 1,3087 vyjádříme jako 13 087 / 10 000 a rovnici naprogramujeme takto:

Voltage1_DaOutput = Voltage1_DaMilivolt * 13 087 / 10 000 – 37

Teď už není potřeba knihovna float.h. Číslo 13 087 zabere 14 bitů, vstupní hodnota je 16-ti bitová. Takže pro násobení bude potřeba minimálně 14 + 16 = 30 bitů. Proměnná Votage1_DaMilivolt musí být deklarována jako unsigned long int. Tak překladač (AVR studio) pozná, že si má pro výpočet vyhradit 32 bitů v paměti i když ze samotné proměnné budeme využívat jenom 16 bitů.

Poslední úvaha se bude týkat rychlosti výpočtu. Před a za rovnici jsem v programu dal rozsvícení a zhasnutí LED diody připojené na některém z pinů procesoru. Rovnici jsem nechal opakovaně počítat a na osciloskopu podle blikání ledky měřil, jak dlouho to trvá. Procesor ATxmega na 32MHz potřebuje 20µs na jednu rovnici, ve které je použito dělení 32-bitového čísla.

Operace dělení bude nejspíš z celého výpočtu trvat nejdelší dobu. Proto se pokusíme dělení nahradit posouváním bitů. Když posuneme číslo o 14 bitů do prava, je to stejné, jako když číslo vydělíme hodnotou 16 384. To je 2^14.

2^14 * 1,3087 = 16 384 * 1,3087 = 21 442

Voltage1_DaOutput = (( Voltage1_DaMilivolt * 21 442 ) >> 14 ) – 37

Znovu jsem změřil rychlost počítání a jsme na 5µs. Takže bez dělení je to čtyři krát rychlejší.

Linearita multimetru?

V předchodzích kapitolách jsme uvažovali, že DA převodník s celou analogovou částí zdroje i multimetr, kterým byly získány údaje pro sestavení rovnice jsou lineární. Body pro sestavení rovnice jsme měli jenom dva a zvolil jsem je náhodně. Je to celé lineární, stačí opravdu jenom dva body k sestavení rovnice?

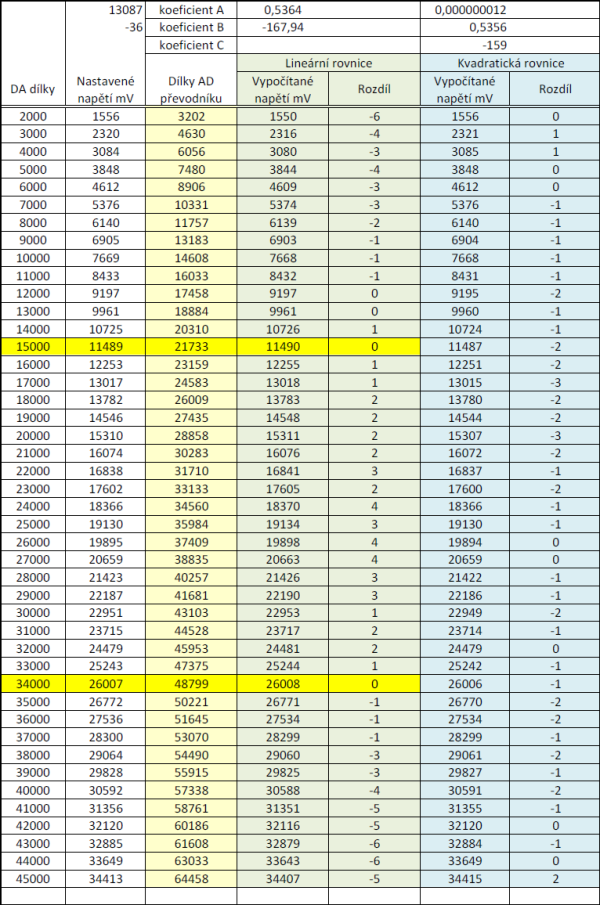
Program zdroje jsem upravil tak, abych bylo možné rotačním kodérem nastavovat hodnotu DA převodníku. Na výstupní svorky zdroje jsem připojil multimetr UT61E a M-3860 a naměřené hodnoty opisoval do tabulky ve voltech.
 

Měření v každém sloupci bylo prováděno třikrát, abych měl jistotu, že zapojení je stabilní a měřidla i při opakovaném nastavení stejné hodnoty na DA převodníku ukážou stejnou hodnotu. Při zátěži a zahřátí už to tak dobré nebude, ale to teď zkoumat nebudu.

Do další dvojice sloupců tabulky jsem napsal rovnice – jejich koeficienty jsou v horní části tabulky. Řádky, podle kterých byly v předchozím článku vypočítány koeficienty rovnic jsou zvýrazněny.

V poslední dvojici sloupců je vypočítána odchylka vypočítané a naměřené hodnoty. Tady uvidíme, jak moc jsou měřidla a DA převodník vůči sobě lineární. Pro stanovení koeficientů rovnice jsem použil údaje z multimetru UT61E. Odchylka mezi naměřeným a vypočítaným je jeden, nebo dva dílky DA převodníku, to je mnohem lepší, než jsem čekal.

Maximální hodnota zobrazená na multimetru UT61E je 22000. Do 22V multimetr ukazuje se stejnou linearitou jako DA převodník spolu s ostatními obvody zdroje. Potom se přepne rozsah a další hodnoty utíkají. Rozsahy měřidla UT61E na sebe nenavazují.

U staršího multimetru Metex M-3860D je vidět podobná změna při přepínání rozsahů někde kolem 4V. Další naměřené údaje jsou vůči DA převodníku zdroje nelineární.

Prozatím nemám k dispozici měřidlo z větším rozlišením, proto nechám rovnici naprogramovanou podle UT61E.
 

Funkce pro AD převodník napětí

AD převodník ADS8343, který jsme použili ve zdroji, má na svém vstupu multiplexer pro přepínání čtveřice vstupů. Jeden z nich je přes dělič sestavený z odporů a operační zesilovač připojen k výstupním svorkám zdroje tak, aby mohl měřit výstupní napětí. Převodník je napájen referenčním zdrojem 2,5V stejně jako DA převodník a jeho rozlišení je 16 bitů. Podobně jako u DA převodníku jsme se nezabývali přesnými hodnotami odporů v děliči, ani offsetem obvodu. Přepočítání jednotek AD převodníku na milivolty zajistí rovnice. Abychom mohli rovnici sestavit, vytvoříme podobnou tabulku jako v předchozí kapitole.

Pro jednotlivá napětí nastavená na DA převodníku, zapíšeme do tabulky hodnoty z AD převodníku (vyznačeno světle žlutě). Koeficienty lineární rovnice potom můžeme vypočítat na papíře, podobně jako v předchozí kapitole. V dalším slouci je rozdíl mezi vypočítanou a nastavenou hodnotou v milivoltech. Je vidět, že obvod AD převodníku není lineární vůči napětí nastavenému na DA převodníku. Zároveň AD převodník není lineární vůči multimetru UT61E. Chyba je +4mV uprostřed rozsahu a -6mV na jeho koncích. Vzhledem k tomu, že multimetr byl použit jenom do 22V, tak nevím, jestli je opravdu nelineární obvod AD převodníku. To bude možné zjistit, až se podaří zapůjčit někde přesnější měřidlo.

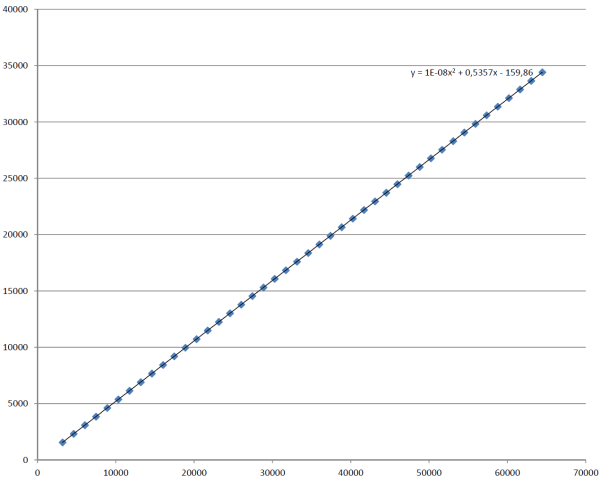
Teď se budu snažit korigovat nelinearitu vyjádřenou rozdílem v zeleném sloupci. Tento problém už neumím vyřešit na papíře, pro další práci jsem použil Excel. Z hodnot v tabulce jsem vytvořil bodový graf. Hodnoty řady X jsou data z AD převodníku, hodnoty řady Y je požadované napětí v milivoltech, které bylo vypočítáno z DA převodníku a naměřeno multimetrem.
 

V grafu je možnost přidat spojnici trendu a vybrat typ regresní funkce. Vybral jsem polynomickou regresní funkci druhého řádu. To je vlastně kvadratická funkce a jejím grafem je parabola. Parabola je v tomto případě prohnutá jenom málo, asi o 10mV na celém rozsahu. Prohnutí je popsáno prvním koeficientem rovnice, který má hodnotu 0,000000012. Koeficienty vypočítal Excel, já to neumím. Podrobněji je problematika práce s regresními funkcemi popsána např. zde. V dalším sloupci tabulky jsem zobrazil rozdíly od požadovaného, abych viděl, jak moc se Excel trefil. Chyba je +2 / -3mV. Rovnice je tady:

Voltage1_AdMilivolt = 0,000000012 * Voltage1_AdInput²

+ 0,5357 * Voltage1_AdInput – 160

Kvadratická regresní funkce na osmibitovém procesoru

Koeficienty přizpůsobíme do tvaru, který je vhodný pro mikroprocesor:

Koeficient 0,000000012 * 2^31 = 26. Takže první část rovnice bude vypadat takto

((( Voltage1_AdInput * Voltage1_AdInput ) >> 6 ) * 26 ) >> 25

Rotaci vpravo jsem samozřejmě mohl provést najednou o 31 bitů a potom násobit koeficientem 26. Jenomže to by většinou nebylo co násobit, protože většina menších čísel by se rotováním vynulovala. Na druhé straně, nemůžu napřed násobit a potom rotovat, protože druhá mocnina 16-ti bitového čísla zabere 32 bitů, takže na násobení už nezbývá prostor v long int. Koeficient 26 potřebuje 5 bitů, já rozdělil rotaci o 31 bitů na 6 + 25.

Koeficient 0,5357 * 2^15 = 17554. Další část rovnice bude

( Voltage1_AdInput * 17554 ) >> 15

Teď už stačí dvě části kvadratické funkce sečíst a přičíst poslední část: -160.
 

Multimetr Fluke8842 a přesnost výsledků

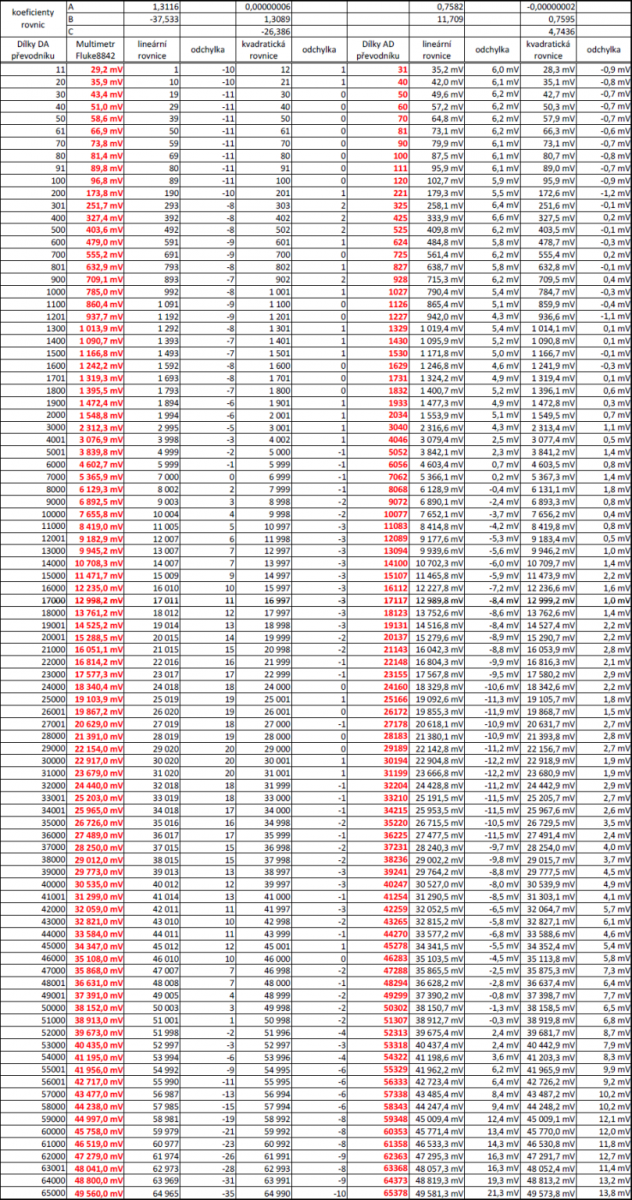
Kolega Michal zapůjčil 5,5 místné stolní měřidlo Fluke8842 a znovu provedl měření až do 50V. Já měl pro testování v předchozích kapitolách jenom 35V transformátor. Nic přesnějšího než Fluke8842 už mít nebudeme, takže tento přístroj je pro nás „ideálně lineární“ a linearitu našich výpočtů se mu budeme snažit přizpůsobit. Předpokládáme přitom, že nelinearity, které jsme měřením objevili, vznikají v obvodech našeho zdroje a proto je musíme kompenzovat rovnicemi v programu procesoru.
 

Na DA převodníku bylo nastavováno to co je v prvním sloupci tabulky. Červeně jsou vyznačeny hodnoty odečítané z multimetru a hodnoty odečítané z AD převodníku pro měření napětí na výstupních svorkách zdroje. V dalších sloupcích jsou lineární a kvadratické rovnice, které používají koeficienty z horní části tabulky. Koeficienty byly získány regresí v Excel. Sloupce s odchylkami vyjadřují rozdíl mezi naměřenou a vypočítanou hodnotou. A jak je to s přesností počítání?

• Lineární rovnice DA převodníku má největší chybu -35 / +20 dílků z 65000. Chyba je 0,05%, nebo 538ppm – 538 miliontin z celého používaného rozsahu převodníku.
• Kvadratická rovnice DA převodníku má chybu -10 / +2 dílky z 65000. Chyba je 153ppm, takže výpočtem jsme se k Fluke přiblížili 3,5x líp, než v předchozím případě.
• Lineární rovnice AD převodníku má chybu -11,5 / +21,3mV z 50.000mV rozsahu zdroje. Chyba je 426ppm.
• Kvadratická rovnice AD převodníku má chybu -0,9 / +13,8mV, to je 276ppm. Tato chyba je hlavně na vysokém napětí, kolem 50V. To je dáno tím, že na malém napětí, do jednoho voltu bylo provedeno hodně měření, aby v té části bylo počítání přesnější – relativní chyba byla menší. Regrese se snaží dosáhnout minimální průměrné odhylky, takže tam kde je větší množství dat, je proložení křivky pečlivější.

Hodnoty byly získány při nezatíženém zdroji, nebo byl zdroj zatížen odporovou zátěží 10 a 20ohm. Při zatěžování zdroje v praxi, bude práce převodníků zatížena různými chybami z proměnlivé zátěže, její indukčnosti atd. V této kapitole jsem chtěl ukázat způsob programování měřidel ovládaných procesorem, bez ohledu na další vlivy reálného zapojení.

Další věcí, kterou bych chtěl zahrnout do výpočtů, je teplotní kompenzace. Máme možnost měřit teplotu ve skříňce zdroje a podle ní upravovat koeficienty rovnic. Toto zatím nemáme jak vyzkoušet, protože desky volně položené na stole se stačí ochlazovat, změny parametrů i při zatížení nejsou moc velké.

Metoda pro zísání další dvojice rovnic pro počítání s proudem je stejná. Spousta měření v režimu zdroje proudu, zapisování do tabulek a potom regresní funkce získané v Excel a naprogramované tak, aby nebylo potřeba dělení.

Časová náročnost výpočtů na ATxmega128

Chtěli bychom, aby informace na displeji zdroje byly obnovovány 10x za sekundu. Takže na jeden cyklus komunikace s deskami, výpočty a přepsání údajů na displeji máme 100ms.

Procesor běží na 32MHz a přepisuje všechny proměnné na TFT displeji s rozlišením 480×272 bodů, to trvá asi 30ms. Přitom se vždy mění jenom některé hodnoty. Takže pokud bychom zjišťovali, co se od minulého přepsání změnilo a co ne, stačila by v průměru třetina času na vykreslení.

Každý ze dvou zdrojů potřebuje 4 rovnice po 5µs, když jsou lineární. Kvadratické potřebují 15µs, takže celkem 15 * 8 = 120us. Potom podle Ohmova zákona počítáme vnitřní odpor zátěže a její příkon. Tam už se nevyhneme operaci dělení, ale stejně se s celým počítáním nedostaneme nad 1ms.

Nějaký čas zabere komunikace po sériovém kanálu, snímání údajů z klávesnice a rotačního kodéru, ale to všechno je řízeno z přerušení, takže procesor nikdy nečeká. Ve srovnání s kreslením na displeji jsou tyto činnosti časově nenáročné.

Zdroj funguje a nás čeká mechanická konstrukce a potom programování různých detailů a funkcí, které námi navržený obvod umožňuje – výkon procesoru je dimenzovaný dost.

Závěr

V článku jsem se snažil podrobně popsat metody sestavení rovnic, které je potřeba programovat nejenom u měření na laboratorním zdroji. Regresní funkce jsou potřeba vždy, když stavíme nějaké měřidlo s mikroprocesorem. Procesor má nějakou naměřenou hodnotu (většinou z AD převodníku), kterou je potřeba přepočítat na jednotky měřené veličiny. Může to být nejenom napětí, ale i teplota, tlak, vzdálenost… Čidla, která převádí měřenou veličinu na napětí, mají vždy nějakou nelineariaritu. Další chyby mohou být vneseny použitými zesilovači, teplotní závislostí součástek…

V dnešní době by stačilo použít excel a na jednočipovém procesoru rovnici opsat do programu s použitím čísel s pohyblivou čárkou. Já si napřed udělal představu o výpočtu na papíře, bez použití počítače. Zkusil jsem, jak by to asi mělo vyjít, abych v dalším, složitějším kroku chápal a uměl odstranit chyby. Až když problematiku pochopím, použiji k přesnějšímu počítání nástroje typu Excel. A nakonec jsem chtěl v článku zopakovat přechod od lidského počítání v desítkové soustavě k tomu, co je optimální pro osmibitový mikroprocesor – z mého pohledu celkem podceňovaná oblast přemýšlení při programování.